皆さまこんにちは!
今回は論理パズル(というより確率論?)の中で超有名な問題「モンティ・ホール問題」について徹底的に解説していきたいと思います。
この問題は数学が得意な人でもきちんと答えられない代わりに、数学が得意でない人でも感覚的に答えられる人がいるという何とも面白い問題となっています。
考えれば考えるほど混乱する問題ですので、この記事を読んでもらったら納得してもらえるように、出来るだけ、丁寧に、解説していきたいと思います。
■モンティ・ホール問題とは
まずはモンティ・ホール問題を紹介しておきましょう。
その問題がこちら。
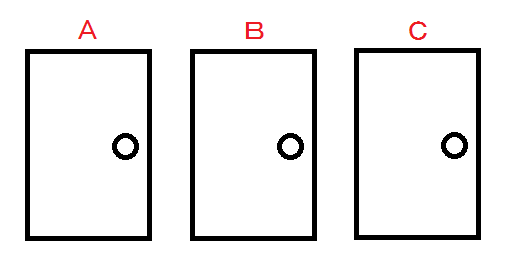
プレーヤーの前に閉じた3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。ここでプレーヤーはドアを変更すべきだろうか?
これを聞くと「答えなんてあるの?」、「どっち選んでも一緒じゃないの?」とパッと見は思ってしまうと思います。
どちらを選んでも確率は1/2、50%:50%の様な気もしますが、先に答えを言いますと、
『ドアを変更すべき』
が答えとなります。
何故、ドアを変更した方がよいのでしょうか?
下記から解説しておきます。
■どちらのドアを選んでも確率は1/2ではない

なぜドアを変更すべきなのかを下記から解説していくのですが、その前にほぼ皆さんがお持ちの考えを取っ払っておきたいと思います。
それは
「どちらのドアを選んでも確率は1/2じゃないか」
という疑問です。
この概念を払しょくしてもらったうえで下記からの解説を聞いてもらうとすんなり頭に入ってくると思います。
この疑問を解決する糸口は2点あります。
- 司会者はどのドアが正解のドアかを知っている
- 最初は3つの扉。その後司会者が不正解のドアを1つオープンし2つに絞る
この2点の条件がある為に単純に50%の確率ではなくなります。
最初からドアが2つしかなく、どちらかのドアを選択した場合はもちろん確率は50:50です。しかし今回の問題は『3つあるドアの中から、正解を知っている司会者が、プレイヤーが選ばなかった2つのドアから1つをオープンさせる』のです。
そこにヒントが隠れています。
少しは「あれ、ちょっと怪しいぞ」と思ってもらえたら、この章はOKです。
■具体的な確率は2/3となる理由

それでは具体的な解説に入ります。
まず、A・B・Cの3つのドアから、プレイヤーはAのドアを選択し、その後司会者がBのドアをハズレとしてオープンしたとします。
まず、3つの扉からプレイヤーがAの扉を選んだ時、Aの扉が正解の確立は1/3です。これは言わずもがなですよね。
逆に言うと、B・Cである確率は2/3となります。
(B:1/3、C:1/3、合わせて2/3)
ここで答えを知っている司会者が登場。B・CからハズレであるBを削除します。
という事はCである確率は、Bが存在していた時の確立2/3を継承しているので、プレイヤーが選択したA:1/3よりも確率的には大きくなる為、ドアを変更した方がよいという結論になります。
★ここがポイント!
司会者はどの扉が正解か知っています。つまりBの扉が外れであることを知った上でオープンします。
Bが正解であればCを、Cが正解であればBをチョイスする事が出来、司会者が正解を知っているが故に、Bの扉が開いた時点での確率は扉が開く前の確立に依存されるわけです。
■母数を増やすとイメージしやすい

ここまで読んでも「アナタ、ナニイッテルカワカラナイ…」と思った方、私の語彙力不足ですいません…
という事でもう少し直感的に分かりやすくしてみたいと思います。
それは『扉の枚数を増やして考えてみる』です。
■問題
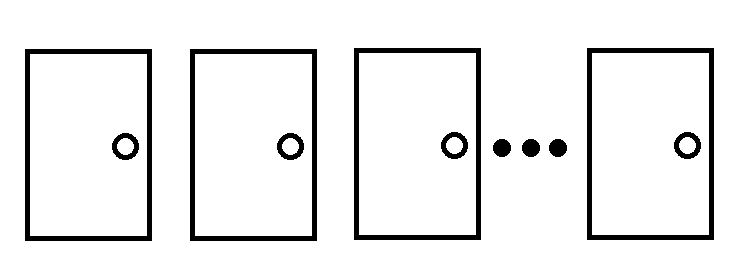
・1万枚の扉からあなたは正解だと思う扉を1枚選びます。
・正解を知っている司会者が残りの9999枚の中からハズレの扉を9998枚オープンさせ、1枚だけ残します。
・あなたは選んだドアを変更しますか?
これならどうでしょうか?
今度は大半の人が「変更する」と直感的に思うのではないでしょうか?
ではなぜそう思うのか?それは前述したように司会者の『意思』が入るからです。
『司会者はどのドアが正解のドアかを知って』います。よって9999個のの扉の中から正解ハズレの分を取り除くことは、逆に言うと「当たりの扉を避けて開いている」という意思がそこには入ります。
したがってプレイヤー側から見た時の確立は、『元の1万個の扉が有る状態のまま、選択肢が2つに絞られた』状態と言いかえることが出来ますので、Aの扉の確率は1/10000、もう片方の扉は9999/10000となります。
■まとめ
いかがでしたでしょうか?
今回は「モンティ・ホール問題を誰でも分かる様に徹底的に解説する。」と題し、確率論と言いながら、論理パズルにも通ずる考え方について解説しました。
この手の問題は脱出ゲーム等にはあまり出てくるような問題ではありませんが、論理パズルや頭の体操系では出てくるような問題です。
頭を柔らかくする上でも常日頃から個の様な変な?面白い?問題に触れておくことは大事だと思いますので、面白そうな問題があればジャンルを問わずにこれからもUPしていきたいと思います。
それでは!





コメント
[…] 掲載元のブログ […]
[…] 掲載元のブログ […]