皆さまこんにちは!
3×3の9つの点を4つの直線で一筆書きで書けるか?という問題を書いていきます。
今回の回答には頭の柔軟さがかなり必要になりますので、頑張って解いてみてください。
■今回の問題

今回の問題はこちらです。
下記の様な9つの点が縦横3×3で正方形に並んでいます。
この点を全て通るように一筆書きで4つの直線で通ってください。

さて、あなたはこの謎が解けるでしょうか?
■ヒント等
この問題、色々やってみると分かりますが、基本的に4本の直線では9個の点は結べません。
必ず最後に1個点が残ります。
ここで必要なのは頭の柔らかさです。
そしてヒントとしては「枠に囚われない考え方」です。
いいですか、「枠にとらわれずに」解いてください。
時間のある方はこの先を読まずに考えてみてください。
解けるとスッキリしますよ!
ヒント1でもわからなかった皆さん、それではヒント2です。
まずは最初にペンを置く場所を決めます。
答えにたどり着く道は何か所かありますが、一旦左上を最初においてください。
そのまま右下の点まで線を引いてください。これが1筆目。
そこから2筆目は左下の点に向かってに進んでください。
そのまま左下の点の上で止まる?いえ、左下の点を通り越してもう少し線を伸ばしてみてください。そう、ここがヒント1で話をした「枠にとらわれない」と話していた部分になります。
ヒント2はここまでです。
■謎を解いていく
さて、それでは謎を解いてきましょう。
まず、ヒント1でも書きましたが、普通に解いてみると必ず1個点が残り、4本の線では結べません。
例えばこんな感じ↓。
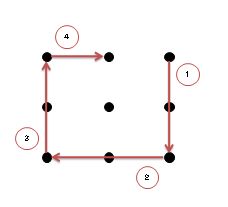
真ん中の一点が残ってしまい、5本目の線が必要となってしまします。
どこからスタートしようが、どう線を折り曲げてみようがこれは変わりません。
では、どうすればよいのか。
それは、「点で線を止めずに突き抜ける事」です。
つまりは下記のようにします。
①まずは左上の点から右下の点に直線を引きます。
②その後左におり曲がり左下の点まで伸ばすのですが、そこで止まるのではなくそのまま突き抜けます。
③そして左真ん中と上真ん中が一直線になるまで直線の先端を伸ばし、おり曲がります。
④同じく上真ん中の点を突き抜け、右列と同じ位置まで来たら、下におり曲がり点を結べば完成です。
絵で見てみると下記が答えです。
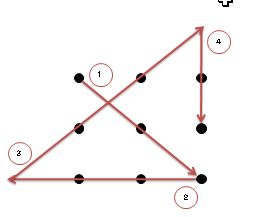
②から③の部分がこの問題における最重要ポイントですね。
9つの点が出てきたときに勝手にこの9個の点に枠をつけてしまって考えてしまうと、永遠に答えにたどり着けません。
色々な視点から物事をとらえ、虫の目(視点を小さくして物事を見つめる)、鳥の目(俯瞰して物事を見つめる)、魚の目(流れをとらえて物事を見つめる)の3つの目で問題を見てみるといいかもしれません。
今回の場合だと鳥の目(俯瞰)して問題を見てみると、答えにたどり着くきっかけになったかもしれません。
■感想
いかがでしたでしょうか?
皆さんは解けましたか?
私は所見では解けませんでした。というか初見で解ける人、頭柔らかすきでしょ!
ちなみに正解は上の通りですが、私、もっとシンプルな、というか1回も線を折り曲がらずに解ける方法を考えたんですよね。
それがこれ↓

絵で描くと何の事かとお思いかもしれませんが、要は「3つの点が隠れるくらい極太の直線で線を引く」です。
そうすると4本も直線を引かずに1本の直線だけ書けば全て塗れるという…
ダメ?(笑)
いや、正解だってさ、「枠はみ出したらダメって書いてないでしょ?だから突き抜けてもOKなのよ」っていう理由がまかり通るなら、「線の太さの基準なんて書いてないでしょ?だから極太の線でも問題ないでしょ。」っていう理由もまかり通るのではないかと…
頭の体操としてはこちらも正解だと思うのです。
いや、むしろ別解で120点でしょ!
いかがでしょうか?
それでは!



コメント